sohotaya.blogg.se - Nishio sudoku strategy

#NISHIO SUDOKU STRATEGY UPDATE#
#NISHIO SUDOKU STRATEGY MANUAL#
#NISHIO SUDOKU STRATEGY TRIAL#

In technical use the term is avoided because of ambiguity with boxes.

Square – Another word for a cell of a Sudoku.

Also refer to automorphic for a type of symmetry where the digits (not just their positions) play a role in another type of symmetry.

In addition, groups of clues can display other types of symmetry, such as translational symmetry. reflection symmetry on two diagonal axes.reflection symmetry on one diagonal axis.reflection symmetry on two orthogonal axes.reflection symmetry on one orthogonal axis.Symmetry – A Sudoku can have seven types of overall symmetry in its clue positions.Translational symmetry (each clue group takes the form n, n+1, n+2, n+3), (24 clues). Size – Refers to the size of a puzzle or grid, and can be described as a composite (i.e.

#NISHIO SUDOKU STRATEGY TRIAL#

Note: the level of trial and error is usually not explicitly defined.

Satisfactory puzzle – A puzzle that does not require trial and error (guessing).

In some variants regions are not equally shaped. Region – Another term for the boxes of a Sudoku.Sudokus are always expected to be proper Sudokus unless the puzzle setter specifies otherwise. Proper Sudoku – A Sudoku with one solution.In some variants nonets are not equally shaped. Nonet – Another term for the boxes or regions of a Sudoku.(See Mathematics of Sudoku – Minimum number of givens for details). Minimum number of clues – Refers to the minimum of all proper Sudokus.Different minimal Sudokus can have a different number of clues. Minimal – A minimal Sudoku (or irreducible Sudoku) is a Sudoku from which no clue can be removed leaving it a proper Sudoku (has one solution).Latin square – A related puzzle, or number array, with only row and column constraints (omitting the box constraint).In large Sudokus, such as "Sudoku the Giant", elements may be alphanumeric, or a larger set of numbers, e.g. This term is often used in a mathematical context, especially for Sudokus larger than 9×9, when more than nine digits "1-9" are required. Element – A digit or number of the Sudoku.Constraints – The rules of a Sudoku that require each digit to appear only once in each row, column, and box.In solving most Sudokus, this is usually a poor approach, but in the most difficult examples may be necessary. backtracking) and making a different guess.

#NISHIO SUDOKU STRATEGY MANUAL#

In the manual form, it indicates the effort of making a guess, and if found to be wrong, going back (i.e.

Backtracking – A programming method to solve Sudokus, but can also describe a manual method.

Automorphic – A property of some Sudokus where the digits (not just their positions) play a role in a type of symmetry.

There are puzzles at the highest difficulty that cannot be solved without guessing, and indeed some have more than one solution (depending on who made it and how diligently it was designed.An automorphic Sudoku. I did this with one hand on my phone because my 5-month-old refuses to not be held and walked around the house. Using this as a starting point, I was able to logically fill out the rest of the puzzle:

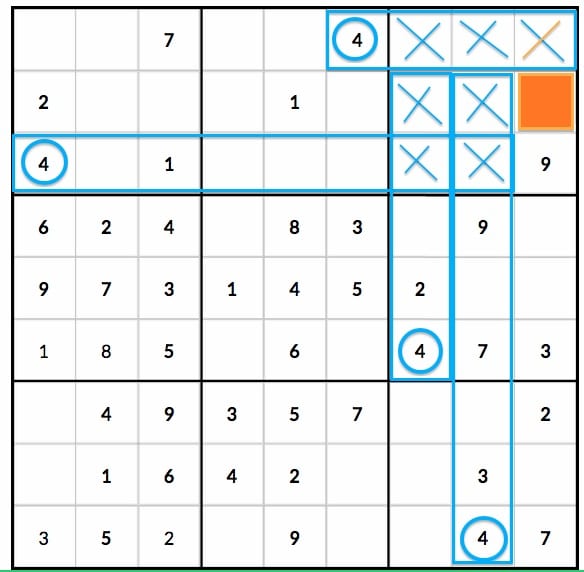
These 4 positions are coupled together, forcing an additional elimination. I don't have any other name for it, but the way I see it You can see here, regardless of whether you put 4 or an 8 in r2c1, r3c5 will be the other, which means (without guessing) you know r3c3 cannot be a 4. You find couples of pointing pairs that are linked together in a set of 4, which regardless of which number is placed in it can also eliminate candidates. For those unaware of what "pointing pairs" are (like I was, even though I used the method) here's a link to information on that.

#NISHIO SUDOKU STRATEGY UPDATE#

So I'll update the rest of the answer from here to explain what I did in addition. Others have pointed out the correct start point but not linked it to a method.Īfter comment and further review I see that my method is just an extension of pointing pairs, which was already employed on the puzzle.